2019 중앙대 수리논술 자연계1 문제 및 풀이/해설/분석 (2021 논술 기준)
안녕하세요! 의대생 현이입니다.
오늘은 어제 카페에서 말했다시피 2019 중앙대 자연계1 수리논술 문항 3개에 대해 풀이 및 분석을 할 예정입니다.
스포를 방지하기 위해 문항을 우선 풀어보고 오시는 것을 추천드립니다.
혹시 문제를 아직 복사하지 못하신 분은 제가 카페에 업로드를 해 둔 캡쳐 사진 3개를 복사하고 풀어본 후에 이 글을 다시 보는 것을 추천드립니다.
2019 중앙대 자연계1 수리논술 3...
대한민국 모임의 시작, 네이버 카페
cafe.naver.com
(이 글에서는 절대 문제 전체를 올리지 않을 것이니 복사하고 꼭 풀어보시고 글을 봐주세요!)
일단 1번 문제 부터 살펴보겠습니다.

중앙대는 거의 항상 1번 문항을 확률과 통계를 출제하는데요.
확통 문제 같은 경우 조건 해석이 가장 중요하다고 볼 수 있습니다.
문제는 철수와 영희가 각각 게임에 참여해 빨간 주머니에서 철수는 1번 공을, 영희는 2번 공을 뽑았을 때 서로의 점수가 상대 점수보다 높을 확률을 각각 구하라는 문제입니다.
규칙을 해석을 해보면 결국 변수 a와 b에 따라 직선의 그래프가 정해지고, 해당되는 넓이를 따지면 되는제 문제 제시에서 철수와 영희의 a에 대한 값을 준 것입니다.
그럼 결국에는 조건에 따라서 값을 구하고 경우의 수를 찾으면 되는 것입니다.

케이스에 따른 값은 잘 구하시면 제가 써 놓은대로 나오실 것입니다.
그럼 이제 철수가 영희보다 더 높은 점수를 얻을 확률과 영희가 철수보다 더 높은 점수를 얻을 확률 각각의 값은 어렵지 않게 나올 수 있습니다. (총 경우의 수가 25개이고, 철수가 영희보다 점수가 높은 경우의 수는 총 8개, 영희가 철수보다 점수가 높은 경우의 수는 15개입니다)
사실 중앙대 수리논술 1번 문항은 무조건 맞춰야 하는 문항이고 우스갯소리로 "중앙대 수리논술 1번 문항을 못 풀거나 틀리면 뒷 문항은 채점도 안한다더라"라는 말까지 있을 정도입니다.(팩트는 아닙니다.)
중앙대 1번 문항은 항상 이런식으로 케이스 나열하고 간단하게 결과를 도출하는 문제가 많으므로 평소에 경우의 수 문제를 푼다는 느낌으로 하시면 될거 같습니다.(단, 서술은 빡시게 해야겠죠)
다음 문제 살펴보겠습니다.

제시문은 짜르고 문제만 올려두었는데요. 실제로는 제시문 꼭 체크해 주셔야 합니다.
(블로그 포스팅 길이를 생각해서 짤랐습니다. 그러니까 꼭 미리 복사해서 먼저 풀어봐주세요 ㅠ)
제시문에서는 tan함수의 덧셈정리와 극한의 곱셈법칙 그리고 부분적분에 대한 식이 있습니다.
제가 항상 강조하는 것인데, 문제를 풀 때 제시문 무조건 활용해주셔야 합니다.
그걸 유의하면서 2-1번 문제를 봐보면, 세 점사의 각의 최대를 구하는 문항이므로 "아! 탄젠트 덧셈정리 또는 뻴샘정리를 꼭 이용해 주어야 겠구나!"를 추론할 수 있습니다.

그림으로 표현하면 대강 이런 형태가 되구요. 결론적으로 tan 공식을 활용하면 구하려는 tan에 대한 식은 x와 관련된 식으로 나올 겁니다. 그리고 그 식에 대해 분모의 최소를 구하는 미분을 써도 되긴하지만 산술평균을 쓰는 것이 더 좋습니다.
( 구하는 tan값은 x/5x^2+33x+60이고 분모와 분자 모두 x로 나누고 나서 산술평균 써주면 됩니다. 그럼 tan값이 최대가 되는 x의 값이 2루트3 이라는 것을 알 수 있습니다.)
다음 2-2번 문제를 보겠습니다.
제시문 3개 중 하나를 썻기 때문에 나머지 2개에 대한 것은 이 2-2에서 꼭 사용해주어야겠죠.
일단 기본적으로 제시문에서 부분적분 나왔으니 그걸 먼저 활용해주고 그 결과에서 나오는 식에 대해 제시문에 나온 극한의 법칙을 사용해 주시면 어렵지 않게 답을 도출 시킬 수 있습니다.
다른 것은 다 어렵지 않게 하실거 같은데, 부분 적분이 두번 사용해야 해서 그 부분만 필기 정리해서 보여드리겠습니다.
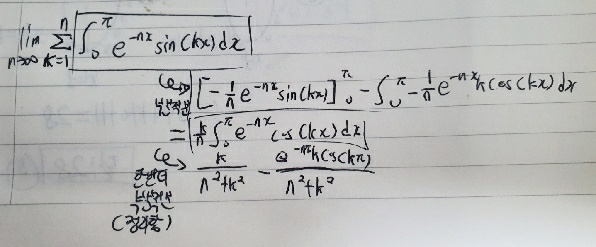
두 번 부분적분한 이 식 앞에 있는 시그마와 lim까지 있으므로 제시문을 이용해 두 식을 쪼개고 정적분으로 바꾸는 공식을 써주면 결과를 도출할 수 있습니다.
(만약 이 부분이 안되시면 카페의 논술 피드백 게시판에 질문 남겨주시면 됩니다. 등급 때문에 안되시면 가입인사 게시판에다가 "블로그 보고 왔는데 질문하고 싶은데 등업 부탁드립니다!" 하면 등업 시켜드리겠습니다. 링크는 글 맨 밑에 걸어두겠습니다.)
어쨋든 구하는 값은 ln2/2입니다. (ln2 나누기 2)
양을 줄이려고 마음먹고 쓰고 있는데도 포스팅이 길어지네요... 3번 문제를 보려고 하는데, 사실 이런 유형이 이제는 나올까 싶습니다. (합성함수와 몫과 차수에 대한 부분이 현 개정에서 크게 비중이 없는 부분인지라...)
그래서 출제 가능성이 높지 않다고 판단되므로 이렇게 문제를 풀면 된다! 정도만 이야기를 하겠습니다.

3-1번 문제는 아마 고1 과정에서 자주 나오던 그런 유형일겁니다.
다항식의 나눗셈을 활용한 몫과 나머지로 구분하여 식 작성을 하고 미지수 컨트롤을 해주면 됩니다.
저는 이런 문제는 올해는 안 나올 것이라고 생각을 하고 있습니다.
(이러고 나오면 곤란하니까... 어쨋든 기출이므로 공부는 해두세여! ㅎㅎ 문제 풀다 막히시면 지문해주시구요!)
3-2번 문제는 C(x,y)로 놓으면 거리 공식을 통해 관계식이 도출이 되겠죠!
근데 어쩌지... 이 식이 결국에는 이차곡선인데.. 올해는 기하가 빠졌네요 ㅎㅎ..
결론: 올해는 3-2번 문제는 나올 확률이 없다! (이건 3-1과 다르게 확률이 0퍼이므로 안 푸셔도 됩니다)
자 이 밑부터는 기하가 포함된 2022 및 그 이후 수능을 준비하시는 학생들만 봐주세여!
어쨋든 접점 공식을 이용하든, 음함수의 미분법을 이용하든 북치고 당구치고 하다보면 기울기가 나오고 그럼 법선의 기울기도 어렵지 않게 도출이 됩니다. 그리고나서 조건에 따라 직선의 기울기에 대한 tan값이 어떤 조건을 만족해야 하는지를 구하시면(그림 활용하셔도 좋습니다) 어떤 식을 써야하는지가 나올겁니다.
그리고 마지막은 항상 그랬다시피 삼각함수를 컨트롤할 수 있는 현 수능 범위에서의 유일한 도구인 덧셈정리를 이용해주시면 됩니다.
여기까지 2021 중앙대 논술에 맞춘 2019 중앙대 수리논술 문제 분석을 해보았습니다.
올해 범위가 많은 변화가 있어서 혼란이 오시는 분들이 있을텐데요.
제 생각에는 올해 중앙대는 확통 1문항/ 수열 1문항/ 미적 1문항 정도 나오지 않을까 생각합니다.
기하가 빠진 부분을 수열이 매꾸는 형태로 진행될거 같고 만약 4문제 나온다면 미적이 1개 추가되겠죠!!
그렇게 복잡하게 생각하실 필요 없고 과거 기출 푸실 때만 기하 제외에 유념하면서 문풀 진행하시면 될거 같습니다 ㅎㅎ
긴 글 읽어주셔서 감사드리고 질문이나 학습 고민, 논술 피드백 등은 카페를 이용해주세요!
(앞에서도 말했지만, 등급 때문에 질문이 힘드시면 가입인사 게시판에 등업 요청글 하나만 써주시면 됩니다)
의대생 현이(전 수만휘 멘토, 강제탈... : 네이버 카페
수능,내신,학종,논술 등에 대한 정보 공유 및 학습 질문 해결을 위한 공간입니다.
cafe.naver.com
'수학(수능,논술)' 카테고리의 다른 글
| 2020 연세대 모의논술 1번 문제 분석(연세대 수리논술 문항 풀이) (0) | 2020.08.23 |
|---|---|
| 2021 경희대 수리논술 대비 기출 문제 특징에 대해 (기하가 빠짐) (0) | 2020.08.09 |
| 2021 논술 전형 대비 대학별 수리논술 문제 추세에 대해(연세대, 중앙대, 경희대 기출 예시) (0) | 2020.07.30 |
| 고등수학 수능/내신 문제집 쎈 특징과 활용법(수1,수2,미적,확률과 통계) (0) | 2020.07.28 |
| 2020 7월 모의고사 (2021학년도) 고3 수학 나형 문제 분석 및 정답과 해설 (0) | 2020.07.25 |



