지수함수 그래프 개념(평행이동,대칭이동) 및 기출 문제 풀이
안녕하세요. 의대생 현이입니다!
오늘은 지수함수에 대한 개념 및 문풀에 대해 이야기를 해 보려고 합니다^^
오늘은 우선 그래프와 평행이동, 대칭이동에 대해서 알아보고 다음 포스팅에서는 최대최소에 대해서 이야기를 마저 해보겠습니다. (사실 한번에 쓰고 싶었는데 너무 양이 많아질거 같아서 둘로 쪼개는 것을 선택했습니다.)
난이도를 너무 올리기보다는 개념 수준의 설명과 간단한 문제 풀이까지 진행해 보겠습니다~
일단 지수함수의 그래프를 잠깐 설명을 해보겠습니다 ㅎㅎ

지수함수 그래프는 기본적으로 밑의 범위에 따라 두 가지의 개형으로 나뉘어집니다.
그에 따라서 몇가지 성질이 나타나는데요!
밑이 1보다 클때는 x가 음의 무한대로 갈 때 0으로 수렴하고, 밑이 커질수록 그래프가 y축과 가까워집니다.
반대로 밑이 1보다 작을때는 x가 무한대로 갈 때 0으로 수렴하고, 밑이 작아질 수록 그래프가 y축과 가까워져요!
그 다음 지수함수의 평행이동과 대칭이동을 살펴보겠습니다.

일단 식은 이렇게 변화가 되는데요! 그래프는 이에 맞춰서 그냥 그려주시면 됩니다.
(변화된 그래프를 그리는 것은 이 글을 보시는 학생 분들의 몫으로 남겨두겠습니다~)
여기까지 일단 관련 개념에 대해 살짝 이야기를 해 보았습니다.
관련 평가원 기출 문제 한 개만 딱 풀어보고 오늘 포스팅을 마무리 해 보겠습니다.

사실 지수함수에 관련된 개념은 그렇게 어렵지는 않지만, 실제로는 그래프 개형 컨트롤 문제가 주로 등장하므로 난이도 자체는 중 정도는 됩니다. (개념과 문제의 괴리가 크고, 보통 일반 4점 난이도로 많이 출제가 되는 편입니다.)
이 문항 같은 경우 그래프의 개형에 따른 교점의 좌표의 범위를 활용해서 해결하는 문제입니다.
그래프가 문제에 나와있기 때문에 아무래도 이를 이용하면 좋을거 같습니다!
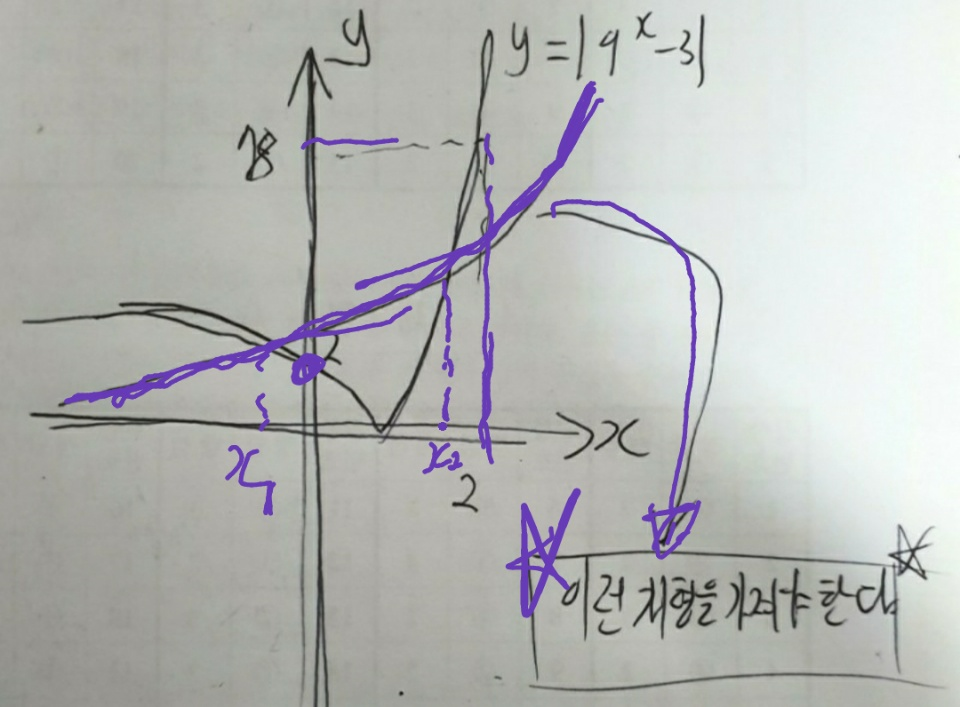
그림이 약간 비주얼적으로 별로인데, 결국 저런식으로 그래프가 형성이 되어야 조건을 만족할 수 있습니다.
이를 식으로 환산해보면 2^k는 2보다 크지만 2^2+k 는 78보다 작아야 저런 그래프가 됩니다.
이를 만족하는 자연수 k의 값은 하나씩 대입을 해보면 2,3,4이므로 답은 2번입니다~
여기까지 지수함수 그래프 및 평행/대칭이동에 관련된 개념과 관련 문제를 살펴보았는데요!
이 글이 개념 습득에 있어서 도움이 되었으면 좋겠습니다.
궁금한 점이나 입시 관련 고민이 있으시면 제가 운영하는 네이버카페에서 질문을 해주시면 감사하겠습니다.
<항상 제 포스팅을 봐주시는 모든 분들, 특히 제 글에 대해서 응원을 아끼지 않으시는 카페 회원 분들께 항상 감사하다는 인사를 드리고 싶습니다. 앞으로도 더 좋은 글을 쓰기 위해 노력하겠습니다.>
'수학(수능,논술)' 카테고리의 다른 글
| 2021학년도 대학별 수리논술 고사 일정(연세대, 한양대,성균관대 등) (0) | 2020.05.26 |
|---|---|
| 지수함수 최대최소 개념 설명 및 관련 기출 문제 풀이 (0) | 2020.05.07 |
| 수리논술 전형 준비 언제부터 해야할까? + 수리논술 학원 선택가이드(feat. 대치동) (2) | 2020.04.29 |
| 2021 ebs 수능특강 수학(미적분,수학1,수학2,확률과통계) 연계 공부방법! (0) | 2020.04.25 |
| 수리논술 전형 준비하는 방법(대학교 기출 문제 및 해설과 채점 기준표에 공부법이 담겨있다) (0) | 2020.04.20 |



